Bài tập 14 trang 213 SGK Toán 12 NC

Bài tập 14 trang 213 SGK Toán 12 NC

a) Đặt \(x = \tan t \Rightarrow dx = \frac{1}{{{{\cos }^2}t}}dt\)

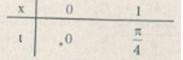
\(\int \limits_0^1 \frac{{dx}}{{{x^2} + 1}} = \int \limits_0^{\frac{\pi }{4}} \frac{{dt}}{{{{\cos }^2}t({{\tan }^2}t + 1)}} = \int \limits_0^{\frac{\pi }{4}} dt = \frac{\pi }{4}\)

b) Ta có:

\(I = \int \limits_0^1 \frac{{dx}}{{{x^2} + x + 1}} = \int \limits_0^1 \frac{{dx}}{{{{(x + \frac{1}{2})}^2} + {{(\frac{{\sqrt 3 }}{2})}^2}}}\)

Đặt \(x + \frac{1}{2} = \frac{{\sqrt 3 }}{2}\tan t\)

\( \Rightarrow dx = \frac{{\sqrt 3 }}{2}(1 + {\tan ^2}t)dt\)

\(I = \int \limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} \frac{{\frac{{\sqrt 3 }}{2}dt}}{{\frac{3}{4}}} = \frac{4}{3}.\frac{{\sqrt 3 }}{2}.\frac{\pi }{6} = \frac{{\sqrt 3 \pi }}{9}\)

c) Đặt 

\(\left\{ \begin{array}{l}
u = {x^2}\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = 2xdx\\
v = {e^x}
\end{array} \right.\)

Do đó:

\(\begin{array}{l}
\int \limits_0^1 {x^2}{e^x}dx = {x^2}{e^x}|_0^1 - 2\int \limits_0^1 x{e^x}dx\\
 = e - 2\int \limits_0^1 x{e^x}dx( * )
\end{array}\) 

Đặt

\(\left\{ \begin{array}{l}
u = x\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = {e^x}
\end{array} \right.\)

Suy ra:

\(\int \limits_0^1 x{e^x}dx = x{e^x}|_0^1 - \int \limits_0^1 {e^x}dx = e - {e^x}|_0^1 = 1\)

Từ (*) suy ra: \(\int \limits_0^1 {x^2}{e^x}dx = e - 2\)

-- Mod Toán 12