Bài tập 6 trang 146 SGK Giải tích 12

Bài tập 6 trang 146 SGK Giải tích 12

Phương pháp:

Câu a, vận dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất trên bậc nhất.

Câu b, phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại tiếp điểm M(x0,y0) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng:

\(y-y_0=f'(x_0)(x-x_0)\)

Câu a:

Khi m = 2, ta thu được hàm số \(y=\frac{x-2}{x+1}\).

Tập xác định: D = R\ {-1}.

Giới hạn:

\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }\frac{x-2}{x+1}=1; \lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{x-2}{x+1}=1\)

\(\lim_{x\rightarrow (-1)^-}y=\lim_{x\rightarrow (-1)^-}\frac{x-2}{x+1}=+\infty ; \lim_{x\rightarrow (-1)^+}y=\lim_{x\rightarrow (-1)^+}\frac{x-2}{x+1}=-\infty\)

Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang là các đường thẳng x= - 1 và y = 1.

Sự biến thiên:

\(y'=\frac{(x+1)-(x-2)}{(x+1)^2}=\frac{3}{(x+1)^2}>0,\forall x\ne 1.\)

Bảng biến thiên:

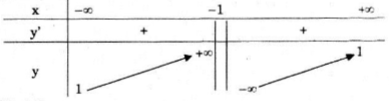
Hàm số đồng biến trên các khoảng \((-\infty ;-1)\) và \((-1;+\infty )\).

Hàm số không có cực trị.

Đồ thị hàm số:

Đồ thị hàm số nhận điểm (-1;1) làm tâm đối xứng.

Đồ thị hàm số cắt trục Ox (2;0) và cắt Oy tại (0;-2).

Đồ thị:

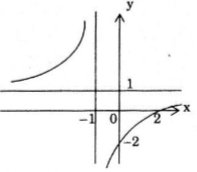
Câu b:

Tiếp tuyến với (C) tại điểm M có hoành độ a, a \(\neq\) -1, có hệ số góc:\(k=f'(a)=\frac{3}{(a+1)^2}\)

Vậy phương trình tiếp tuyến đó là:

\(y-f(a)=f'(a)(x-a)\Leftrightarrow y=\frac{a-2}{a+1}=\frac{3}{(a+1)^2}(x-a)\)

\(\Leftrightarrow y=\frac{3}{(a+1)^2}(x-a)+\frac{a-2}{a+1}\).

-- Mod Toán 12