Bài tập 2 trang 145 SGK Giải tích 12

Bài tập 2 trang 145 SGK Giải tích 12

Phương pháp:

Câu a, áp dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba.

Câu b, áp dụng công thức tính diện tích hình phẳng bằng tích phân.

Lời giải:

Ta có lời giải chi tiết câu a, b bài 2 như sau:

Câu a:

Khi a = 0 ta có hàm số \(y=-\frac{1}{3}x^3-x^2+3x-4\)

TXĐ: D = R.

Giới hạn:\(\lim_{x\rightarrow -\infty }y=+\infty , \lim_{x\rightarrow +\infty }y=-\infty\)

Sự biến thiên:

\(y=-x^2-2x+3; y'=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=1 \ \ (y=-\frac{7}{3})\\ x=-3 \ \ (y=-13) \end{matrix}\)

Bảng biến thiên:

Hàm số đồng biến trên khoảng (-3;1); nghịch biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( {1; + \infty } \right).\)

Cực trị: Hàm số đạt cực đại tại x=1, giá trị cực đại \(y_{cd}=-\frac{7}{3};\) Hàm số đạt cực tiểu tại x=-3, giá trị cực tiểu y_ct=-13.

Đồ thị hàm số:

+ Tính đối xứng: Ta có y'=-2x-2; y'=0⇔ x=-1. Vậy hàm số nhận điểm \(\left ( -1;-\frac{23}{3} \right )\) làm tâm đối xứng.

+ Đồ thị hàm số cắt trục Oy tại điểm (0;-4). 

+ Đồ thị hàm số đi qua các điểm \(\left ( -4;-\frac{32}{3} \right )\) và \(\left ( 2;-\frac{14}{3} \right )\)

+ Đồ thị của hàm số:

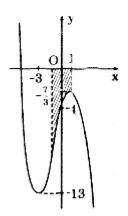
Câu b:

Diện tích hình phẳng cần tìm là:

\(S=\int_{-1}^{1}\left | -\frac{1}{3}x^3-x^2+3x-4 \right |dx= \int_{-1}^{1}\left ( \frac{1}{3}x^3+x^2-3x+4 \right )dx\)

\(=\left ( \frac{1}{12}x^3+\frac{1}{3}x^3-3\frac{x^2}{2} +4x\right )\bigg |^1_{-1}= \frac{26}{3}\) .

-- Mod Toán 12