Bài tập 5 trang 134 SGK Giải tích 12
Bài tập 5 trang 134 SGK Giải tích 12
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:
a) |z| = 1.
b) |z| ≤ 1.
c) 1 < |z| ≤ 2.
d) |z| = 1 và phần ảo của z bằng 1.
Phương pháp:
Đặt \(z=x+yi (x,y\in\mathbb{R})\) khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
Dựa vào dữ kiện đề bài ta xác định tập hợp các điểm biểu diễn số phức z.
Lời giải:
Ta có lời giải chi tiết câu a, b, c, d bài 4 như sau:
Câu a:
Đặt \(z=x+yi (x,y\in\mathbb{R})\)
Ta có |z| = 1 ⇔ 
= 1 ⇔ x2 + y2 = 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1.
.PNG)
Câu b:
Ta có |z| ≤ 1 ⇔ ≤ 1 ⇔ x2 + y2 ≤ 1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn x2+y2=1).
.PNG)
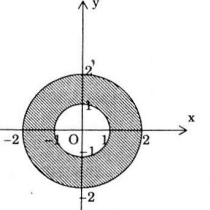
Câu c:
Ta có 1<|z| ≤ 2 ⇔ 1 < ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này).
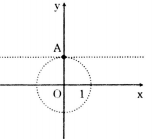
Câu d:
Ta có |z| = 1 ⇔ = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1.
Suy ra x = 0 và y = 1.
Vậy tập hợp các điểm cần tìm là điểm A(0;1).
-- Mod Toán 12
Copyright © 2021 HOCTAP247