Bài tập 1 trang 145 SGK Giải tích 12

Bài tập 1 trang 145 SGK Giải tích 12

Phương pháp:

Với câu a, ta chỉ cần chứng minh biệt thức \(\Delta\geq 0\) thì suy ra được phương trình đã cho luôn có nghiệm thực.

Với câu b, áp dụng định lý Vi-et ta xây dựng được công thức tính S và P, từ đó ta tiến hành khảo sát sự biến thiên và vẽ đồ thị hàm số. Trong bài 1, các hàm số theo S và P sẽ là các hàm số phân thức bậc nhất trên bậc nhất.

Lời giải:

Ta có lời giải chi tiết câu a, b bài 1 như sau:

Câu a:

Xét phương trình:

ax² - 2(a+1)x + a + 2 = 0 (a \(\neq\) 0)

Ta có: \(\Delta '=\left [ -(a+1) \right ]^2-a(a+2)\)

\(\Delta '= (a^2+2a+1)-(a^2-2a)=1>0, \forall a\)

Vậy phương trình luôn có nghiệm thực

\(x_1=\frac{a+1+1}{a}=\frac{a+2}{a}; x_2=\frac{a+1-1}{a}=1\)

Câu b:

Theo định lí Viet ta có: 

\(\begin{array}{l} S = {x_1} + {x_2} = \frac{{2(a + 1)}}{a}\\ P = {x_1}.{x_2} = \frac{{a + 2}}{a} \end{array}\)

Khảo sát sự biến thiên và vẽ đồ thị hàm số của \(S = 2 + \frac{2}{a}\)

Tập xác định: \(D =\mathbb{R} \backslash \left\{ 0 \right\}\)

\(S' = - \frac{2}{{{a^2}}} < 0,\forall a\ne0\) nên hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right).\)

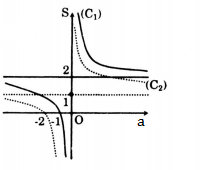
Tiệm cận đứng a=0; tiệm cận ngang S=2.

Đồ thị hàm số giao với Oa tại điểm (-1;0).

Đồ thị hàm số nhận điểm (0;2) làm tâm đối xứng.

Tính tiến đồ thị hàm số \(S = 2 + \frac{2}{a}\) song song với trục tung xuống dưới 1 đơn vị ta được đồ thị hàm số \(P = 1 + \frac{2}{a}\) là phần đồ thị nét đứt trong hình vẽ.

-- Mod Toán 12