Bài tập 12 trang 147 SGK Giải tích 12

Bài tập 12 trang 147 SGK Giải tích 12

Nhận xét:

Đề bài đã cho sẵn cách đặt các biến để thực hiện đổi biến số.

Lưu ý: Khi tính tích phân bằng phương pháp đổi biến số cần thực hiện bước đổi cận.

Lời giải:

Lời giải chi tiết câu a, b, c, d bài 12 như sau:

Câu a:

Đặt \(u=cos\left ( \frac{\pi}{3} -4x\right )\Rightarrow du= 4sin\left ( \frac{\pi}{3} -4x \right )dx\)

\(\Rightarrow sin \left ( \frac{\pi}{3} -4x \right )dx=\frac{du}{4}\)

Đổi cận:

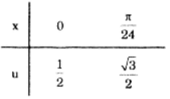
Do đó:

\(\int_{0}^{\frac{\pi }{24}}tan\left ( \frac{\pi }{3} -4x\right )dx=\int_{0}^{\frac{\pi }{24}} \frac{sin\left ( \frac{\pi }{3} -4x\right )}{cos\left ( \frac{\pi}{3}-4x \right )}dx\)

\(=\frac{1}{4}\int_{\frac{1}{2}}^{\frac{\sqrt{3} }{2}}\frac{du}{u}=\frac{1}{4}ln|u| \Bigg |_{\frac{1}{2}}^{\frac{\sqrt{3} }{2}}=\frac{1}{8}ln3\).

Câu b:

Đặt \(x=\frac{3}{5}tant\Rightarrow dx=\frac{3dt}{5cos^2t}\)

Do đó

\(\int_{\frac{\sqrt{3}}{5}}^{\frac{3}{5}}\frac{dx}{9+25x^2}= \int_{\frac{\pi }{6}}^{\frac{\pi }{4}}\frac{3dt}{5cos^2t(9+9tan^2t)}= \frac{1}{15}\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}dt\)

\(=\frac{1}{15} \left ( \frac{\pi }{4}-\frac{\pi }{6} \right )=\frac{\pi }{180}\).

Câu c:

Đặt u = cosx ⇒ du = - sinx dx

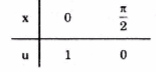
Do đó

\(\int_{0}^{\frac{\pi }{2}}sin^3xcos^4dx=\int_{1}^{0}(u^2-1)u^4du\)

\(=\int_{1}^{0}(u^6-u^4)du=\left ( \frac{u^7}{7}-\frac{u^5}{5} \right ) \Bigg |_{1}^{0}=\frac{2}{35}\).

Câu d:

Đặt \(u=\sqrt{1+tanx}\) hay \(u^2=1+tanx\Rightarrow 2udu=\frac{dx}{cos^2x}\)

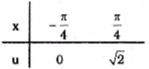
Do đó \(\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{\sqrt{1+tanx}}{cos^2x}dx= \int_{0}^{\sqrt{2}}2u^2du=\frac{2}{3}u^3 \Bigg |_{0}^{\sqrt{2}}=\frac{4\sqrt{2}}{3}\).

-- Mod Toán 12