Bài tập 4 trang 212 SGK Toán 12 NC
Bài tập 4 trang 212 SGK Toán 12 NC
Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lầm in là 50 nghìn đồng. Chi phí để n máy chạy trong một giờ là 10(6n + 10) nghìn đồng.
Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất?
Gọi x là số máy in được sử dụng (x nguyên, 1 ≤ x ≤ 8)
Khi đó, thời gian in 50000 tờ quảng cáo là:
\(\frac{{50000}}{{3600x}}(h) = \frac{{125}}{{9x}}(h)\)
Tổng chi phí để in 50000 tờ quảng cáo là:
\(f(x) = \frac{{125}}{{9x}}(6x + 10).10 + 50x\) (nghìn đồng)
Số lãi sẽ nhiều nhất nếu chi phí ít nhất
Ta cần tìm giá trị nhỏ nhất của f(x) trên [1, 8]
Ta có:
\(\begin{array}{l}
f(x) = \frac{{2500}}{3} + 50x + \frac{{12500}}{{9x}};x \in [1,8]\\
f'(x) = 50 - \frac{{12500}}{{9{x^2}}} = \frac{{50(9{x^2} - 250)}}{{9{x^2}}}\\
f'(x) = 0 \Leftrightarrow x = \sqrt {\frac{{250}}{9}} \approx 5,3
\end{array}\)
Bảng biến thiên:
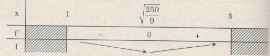
Trên [1, 8] đạt giá trị nhỏ nhất tại \(x = \sqrt {\frac{{250}}{9}} \)
Vì x nguyên nên khi sử dụng 5 máy thì thì thu được nhiều lãi nhất.
-- Mod Toán 12
Copyright © 2021 HOCTAP247
