Bài tập 5.7 trang 220 SBT Toán 12

Bài tập 5.7 trang 220 SBT Toán 12

a) Xét hàm số 

\(f(x) = {e^x} + \cos x - 2 - x + \frac{{{x^2}}}{2}\) 

có tập xác định là R.

\(\begin{array}{l}
f'(x) = {e^x} - \sin x - 1 + x\\
f'(x) = 0 \Leftrightarrow x = 0
\end{array}\)

Ta lại có \(f''(x) = {e^x} + 1 - \cos x > 0,\forall x\) 

vì \(1 - \cos x \ge 0\) và \({e^x} > 0\)

Như vậy, f’(x) đồng biến trên R.

Từ đó: 

\(\begin{array}{l}
f'(x) < f'(0) = 0,\forall x < 0\\
f'(x) > f'(0) = 0,\forall x > 0
\end{array}\)

Ta có bảng biến thiên

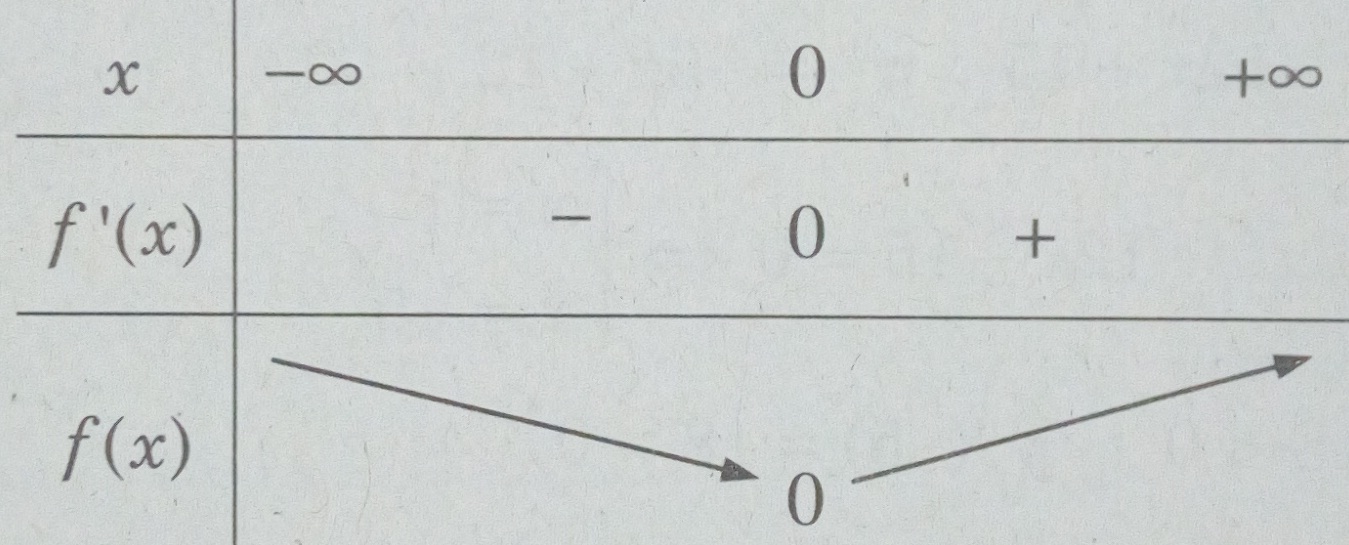
Hàm số 

\(\begin{array}{l}
f(x) = {e^x} + \cos x - 2 - x + \frac{{{x^2}}}{2}\\
 \ge {f_{CT}} = f(0) = 0,\forall x \in R
\end{array}\)

Từ đó suy ra điều phải chứng minh.

b) \(\forall x \ge 0\) xét hàm số

\(f(x) = {e^x} - {e^{ - x}} - 2\ln (x + \sqrt {1 + {x^2}} )\), ta có

\(f'(x) = {e^x} + {e^{ - x}} - \frac{2}{{\sqrt {1 + {x^2}} }}\)

Từ đó f'(x) > 0 với mọi x > 0 

(vì \({e^x} + {e^{ - x}} > 2\) và \(\frac{2}{{\sqrt {1 + {x^2}} }} < 2\))

Và \(f'(x) = 0 \Leftrightarrow x = 0\)

Vậy f(x) đồng biến trên \([0; + \infty )\), tức là:

 \(f(x) \ge f(0) = {e^0} - {e^0} - 2\ln 1 = 0\)

Từ đó suy ra điều cần chứng minh

c) Xét hàm số 

\(f(x) = 8{\sin ^2}\frac{x}{2} + \sin 2x - 2x,\forall x \in (0;\pi ]\)

\(\begin{array}{l}
f'(x) = 4\sin x + 2\cos 2x - 2\\
 = 4\sin x(1 - \sin x)
\end{array}\)

\(f\prime \left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{2}\\
x = \pi 
\end{array} \right.\)

Với \(x \in (0;\pi ]\) ta có \(f'(x) \ge 0\) và dấu bằng chỉ xảy ra tại hai điểm.

Vậy f(x) đồng biến trên nửa \((0;\pi ]\).

Mặt khác, f(0) = 0 nên f(x) > 0.

Từ đó suy ra điều phải chứng minh.

-- Mod Toán 12