Bài tập 6 trang 18 SGK Giải tích 12

Bài tập 6 trang 18 SGK Giải tích 12

Phân tích đề & Phương pháp giải:

Với dạng bài tập này ta sẽ ưu tiên sử dụng quy tắc 2 để giải, sau đó thử lại các tham số tìm được xem yêu cầu bài toán có thỏa mãn hay không.

Tuy nhiên khi rơi vào các trường hợp sau;

Thứ nhất: \(y''(x_0)=0\) với mọi m, không được dùng quy tắc 2 phải chuyển qua dùng quy tắc 1.

Thứ hai: Tính đạo hàm cấp 2 phức tạp, nên ưu tiên sử dụng quy tắc 1.

Lời giải:

Lời giải chi tiết bài 6 như sau:

Xét hàm số \(y = \frac{{{x^2} + mx + 1}}{{x + m}}\)

Tập xác định: \(D=\mathbb{R}\setminus \left \{ -m \right \};\) 

\(y' = \frac{{2{x^2} + 2mx + {m^2} - 1}}{{{{\left( {x + m} \right)}^2}}}\)

Nếu hàm số đạt cực đại tại x = 2 thì \(y'(2) = 0 \Leftrightarrow {m^2} + 4m + 3 = 0\)

\(\Leftrightarrow \left[ \begin{array}{l} m = - 1\\ m = - 3 \end{array} \right.\)

- Với m = -1,  ta có : \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)

\(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}};\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\) 

Bảng biến thiên:

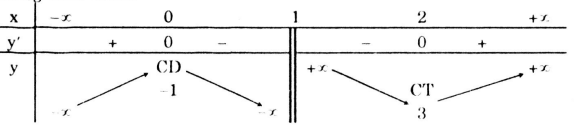
Vậy khi m = -1 hàm số không đạt cực đại tại x = 2.

- Với m = -3, ta có: \(y = \frac{{{x^2} - 3x + 1}}{{x - 3}}\)

\(y' = \frac{{{x^2} - 6x + 8}}{{{{(x - 3)}^2}}};\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 2\\ x = 4 \end{array} \right.\)

Bảng biến thiên:

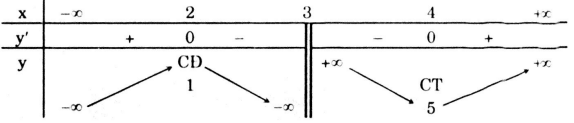
Vậy khi m = -3 hàm số đạt cực đại tại x = 2.

Vậy m = -3 là giá trị cần tìm.

-- Mod Toán 12