Bài tập 3 trang 43 SGK Giải tích 12

Bài tập 3 trang 43 SGK Giải tích 12

Phương pháp giải:

Xét hàm số phân thức: \(y = \frac{{ax + b}}{{cx + d}}\;(c \ne 0,\;ad - bc \ne 0)\)

- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{{ - d}}{c}} \right\}.\)

- Sự biến thiên

+ Tính đạo hàm \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{a{\rm{d - bc}}}}{{{{{\rm{(cx + d)}}}^{\rm{2}}}}}\).

+ y’ không xác định khi \(x = \frac{{ - d}}{c}\); y’ luôn âm (hoặc dương) với mọi \(x \ne \frac{{ - d}}{c}\)

+ Hàm số đồng biến (nghịch biến) trên các khoảng \(( - \infty ; - \frac{d}{c})\) và \((-\frac{d}{c}; + \infty )\)

+ Cực trị: Hàm số không có cực trị.

- Tiệm cận:

+ \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = \frac{a}{c}\) nên đường thẳng \(y = \frac{a}{c}\) là tiệm cận ngang.

+ \(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ - }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\) ;

\(\mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{{ - d}}{c}}^ + }} \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = ( \pm )\infty\) nên đường thẳng \(x = \frac{{ - d}}{c}\) là tiệm cận đứng.

- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

- Đồ thị:

+ Giao của đồ thị với trục Oy: x = 0 ⇒ y = \(\frac{b}{d}\) => (0; \(\frac{b}{d}\)).

+ Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow \frac{{{\rm{ax + b}}}}{{{\rm{cx + d}}}} = 0 \Rightarrow ax + b = 0 \)

\(\Leftrightarrow x = \frac{{ - b}}{a} \Rightarrow (\frac{{ - b}}{a};0)\).

+ Lấy thêm một số điểm (nếu cần) - điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)

+ Nhận xét về đặc trưng của đồ thị. Đồ thị nhận điểm \(I(\frac{{ - d}}{c};\frac{a}{c})\) là giao hai đường tiệm cận làm tâm đối xứng.

Lời giải:

Vận dụng các bước trên ta giải các câu a, b, c bài 3 như sau:

Câu a:

Xét hàm số \(y=\frac{x+3}{x-1}\)

Tập xác định: \(D =\mathbb{R} \backslash \left\{ 1 \right\}\). 

Đạo hàm: \(\small y' = {{ - 4} \over {{{(x - 1)}^2}}} < 0,\forall x \ne 1\).

Tiệm cận:

​\(\small \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty\) 

nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

\(\small \mathop {\lim y}\limits_{x \to + \infty } = 1;\mathop {\lim y}\limits_{x \to - \infty } = 1\) 

nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Bảng biến thiên:

Vậy hàm số nghịch biến trên các khoảng \(\small \left( { - \infty ;1} \right)\) và \(\small \left( {1; + \infty } \right).\)

Hàm số không có cực trị.

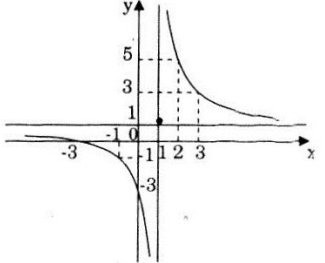
Đồ thị hàm số:

Đồ thị hàm số nhận điểm I(1;1) là giao điểm của hai đường tiệm cận làm tâm đối xứng.

Đồ thị hàm số cắt trục Ox tại điểm (-3;0), cắt Oy tại điểm (0;-3).

Nhận xét: vẫn chưa đủ điểm để vẽ đồ thị hàm số nên ta tiến hành lấy thêm 2 điểm đối xứng với (-3;0) và (0;-3) qua I(1;1) là các điểm (2;5) và (3;3).

Vậy ta có đồ thị hàm số: 

Câu b:

Xét hàm số \(y=\frac{1-2x}{2x-4}\)

Tập xác định: \(D =\mathbb{R} \backslash \left\{ 2 \right\}\).

Đạo hàm: \(\small y' = {6 \over {{{\left( {2{\rm{x}} - 4} \right)}^2}}} > 0,\forall x \ne 2.\)

Tiệm cận:

​\(\small \mathop {\lim y}\limits_{x \to {2^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {2^ + }} = - \infty\) 

nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

\(\small \mathop {\lim y}\limits_{x \to + \infty } = -1;\mathop {\lim y}\limits_{x \to - \infty } = -1\) 

nên đường thẳng y =- 1 là tiệm cận ngang của đồ thị hàm số.

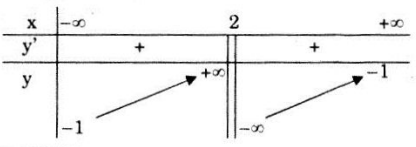
Bảng biến thiên:

Hàm số đồng biến trên khoảng \(\small \left( { - \infty ;2} \right)\) và \(\small \left( {2; + \infty } \right)\).

Hàm số không có cực trị.

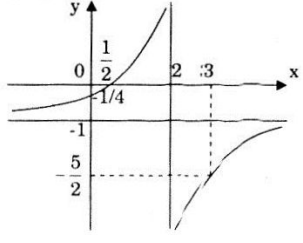
Đồ thị hàm số:

Đồ thị hàm số nhận điểm I(2;-1) làm tâm đối xứng.

Đồ thị hàm số cắt trục Ox tại \(\small \left ( \frac{1}{2};0 \right );\) cắt trục Oy tại \(\small \left (0;-\frac{1}{4} \right );\)

Ta lấy thêm một điểm thuộc nhánh còn lại để vẽ đồ thị hàm số: với x=3 suy ra \(\small y=\frac{5}{2}.\)

Đồ thị hàm số: 

Câu c:

Xét hàm số \(y=\frac{-x+2}{2x+1}\)

Tập xác định: \(D =\mathbb{R} \backslash \left\{ -\frac{1}{2} \right\}\).

Đạo hàm: \(\small y' = {{ - 5} \over {{{\left( {2{\rm{x}} + 1} \right)}^2}}} < 0,\forall x \ne - {1 \over 2}\).

Tiệm cận:

​\(\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} = + \infty\) 

nên đường thẳng \(x=-\frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số.

\(\small \mathop {\lim y}\limits_{x \to + \infty } = - \frac{1}{2};\mathop {\lim y}\limits_{x \to - \infty } = - \frac{1}{2}\) nên đường thẳng \(y=-\frac{1}{2}\) 

là tiệm cận ngang của đồ thị hàm số.

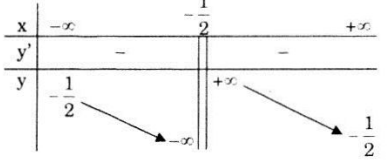
Bảng biến thiên:

Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right).\)

Hàm số không có cực trị.

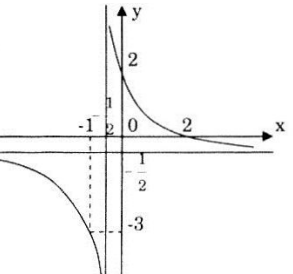
Đồ thị:  

Đồ thị hàm số nhận điểm \(I\left( { - \frac{1}{2}; -\frac{1}{2}} \right)\) làm tâm đối xứng.

Đồ thị hàm số cắt trục Ox tại điểm (2;0), cắt trục Oy tại điểm (0;). Ta lấy điểm (-1;-3) thuộc nhánh còn lại để thuận lợi hơn cho việc vễ đồ thị.

-- Mod Toán 12