Bài tập 9 trang 46 SGK Giải tích 12

Bài tập 9 trang 46 SGK Giải tích 12

Câu a:

\(f(x)=\frac{1}{2}x^4-3x^2+\frac{3}{2}\)

1) Tập xác định: D=R.

2) Sự biến thiên:

Chiều biến thiên: \(f'(x)=2x^3-6x.\)

\(f'(x)=0 \Leftrightarrow 2x^3-6x=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=-\sqrt{3}\\ x=0\\ x=\sqrt{3} \end{matrix}\)

Xét dấu y':

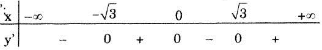
Vậy hàm số đồng biến trên các khoảng \((-\sqrt{3};0)\) và \((\sqrt{3};+\infty )\), nghịch biến trên các khoảng \((-\infty;-\sqrt{3})\) và \((0;\sqrt{3})\).

Cực trị:

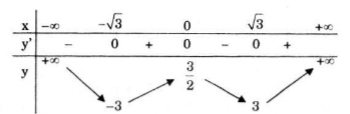
Hàm số đạt cực đại tại x = 0, giá trị cực đại \(y_{CD} = y(0)=\frac{3}{2}\), đạt cực tiểu tại \(x=-\sqrt{3}\) và \(x=\sqrt{3}\), giá trị cực tiểu \(y_{CT}=y(-\sqrt{3})=y(\sqrt{3})=-3\).

Giới hạn:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  - \infty } y\\
 = \mathop {\lim }\limits_{x \to  - \infty } \left( {\frac{1}{2}{x^4} - 3{x^2} + \frac{3}{2}} \right) =  + \infty \\
\mathop {\lim }\limits_{x \to  + \infty } y\\
 = \mathop {\lim }\limits_{x \to  + \infty } \left( {\frac{1}{2}{x^4} - 3{x^2} + \frac{3}{2}} \right) =  + \infty 
\end{array}\)

Bảng biến thiên:

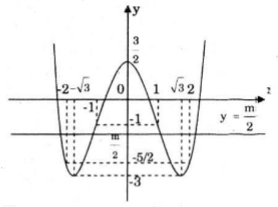
3) Đồ thị

Đồ thị hàm số nhận trục Oy là trục đối xứng.

Đồ thị cắt Oy tại điểm \(\left ( 0;\frac{3}{2} \right )\)

Ta có:

x = 1 ⇒ y = -1

x = - 2 ⇒ y = -5/2

x = 2 ⇒ y = -5/2

x = -1 ⇒ y = -1

Câu b:

Ta có: \(f''(x)=6x^2-6\)

\(f''(x)=0\Leftrightarrow 6x^2-6=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=1 \end{matrix}\)

+ Với  x = -1 ⇒ f(-1) = -1, f'(-1) = 4

Phương trình tiếp tuyến của (C) tại (-1; -1) là:

y = 4(x+1) - 1 ⇔ y = 4x + 3.

+ Với x = 1 ⇒ f(1) = -1, f'(1) = -4

Vậy phương trình tiếp tuyến của (C) tại (1; -1) là:

y = -4(x-1) -1 ⇔ y= -4x + 3.

Câu c:

Ta có:

\(x^4-6x^2+3=m\)

\(\Leftrightarrow \frac{1}{2}x^4-3x^2+\frac{3}{2}=\frac{m}{2}\) (*)

Số nghiệm của (*) là số giao điểm của (C) và đường thẳng \(y=\frac{m}{2}\)

Từ đồ thì (C) ta có:

+ Nếu \(\frac{m}{2}<-3\Leftrightarrow m< -6\) thì (*) vô nghiệm.

+ Nếu \(\bigg \lbrack \begin{matrix} \frac{m}{2}=-3\\ \\ \frac{m}{2}>\frac{3}{2} \end{matrix}\Leftrightarrow \bigg \lbrack \begin{matrix} m=-6\\ m>3 \end{matrix}\) thì (*) có hai nghiệm phân biệt.

+ Nếu \(\frac{m}{2}=\frac{3}{2}\Leftrightarrow m=3\)  thì (*) có ba nghiệm phân biệt.

+ Nếu \( - 3 < \frac{m}{2} < \frac{3}{2} \Leftrightarrow  - 6 < m < 3\) thì (*) có bốn nghiệm phân biệt.

-- Mod Toán 12