Bài tập 69 trang 61 SGK Toán 12 NC

Bài tập 69 trang 61 SGK Toán 12 NC

a) TXĐ: \(D = \left[ { - \frac{1}{3}; + \infty } \right)\)

\(y\prime  = \frac{3}{{2\sqrt {3x + 1} }} > 0,\forall x >  - \frac{1}{3}\)

Hàm số đồng biến trên khoảng \(\left( { - \frac{1}{3}; + \infty } \right)\), hàm số không có cực trị

b) TXĐ: D = [0;4]

\(\begin{array}{l}
y\prime  = \frac{{4 - 2x}}{{2\sqrt {4x - {x^2}} }};\\
y\prime  = 0 \Leftrightarrow x = 2;y(2) = 2
\end{array}\)

Bảng biến thiên

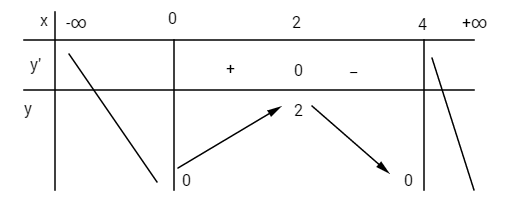
Hàm số đạt cực đại tại điểm x = 2; giá trị cực đại y(2) = 2.

c) TXĐ: \(D = [0; + \infty )\)

\(\begin{array}{l}
y\prime  = 1 + \frac{1}{{2\sqrt x }} = \frac{{2\sqrt x  + 1}}{{2\sqrt x }}\\
y\prime  = 1 + \frac{1}{{2\sqrt x }} > 0,\forall x > 0
\end{array}\)

Hàm số đồng biến trên khoảng \((0; + \infty )\), hàm số không có cực trị.

d) TXĐ: \(D = [0; + \infty )\)

\(\begin{array}{l}
y' = 1 - \frac{1}{{2\sqrt x }}\\
y\prime  = 0 \Leftrightarrow x = \frac{1}{4}
\end{array}\)

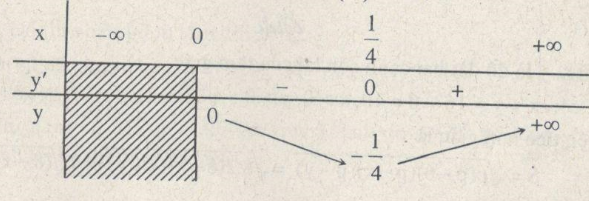
Hàm số đạt cực tiểu tại điểm \(x = \frac{1}{4}\), giá trị cực tiểu \(y\left( {\frac{1}{4}} \right) =  - \frac{1}{4}\)

-- Mod Toán 12