Bài tập 70 trang 61 SGK Toán 12 NC

Bài tập 70 trang 61 SGK Toán 12 NC

Thể tích của hình trụ là: 

\(V = B.h = \pi {r^2}.h \Rightarrow h = \frac{V}{{\pi {r^2}}}\)

Diện tích toàn phần của hình trụ là:

\(\begin{array}{l}
S = 2\pi {r^2} + 2\pi r.h\\
 = 2\pi {r^2} + 2\pi .r.\frac{V}{{\pi {r^2}}} = 2\pi {r^2} + \frac{{2V}}{r}
\end{array}\)

Xét hàm số: 

\(\begin{array}{l}
S(r) = 2\pi {r^2} + \frac{{2V}}{r}(r > 0)\\
S\prime  = 4\pi r - \frac{{2V}}{{{r^2}}} = \frac{{4\pi {r^2} - 2V}}{{{r^2}}}\\
S\prime  = 0 \Leftrightarrow r = \sqrt[3]{{\frac{V}{{2\pi }}}}
\end{array}\)

Bảng biến thiên:

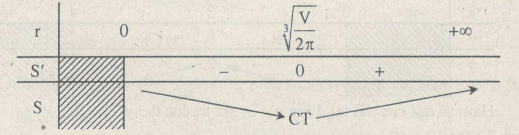
S đạt giá trị nhỏ nhất tại điểm \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\) khi đó:

\(h = \frac{V}{{\pi {r^2}}} = \frac{V}{{{\pi ^3}\sqrt {\frac{{{V^2}}}{{4{\pi ^2}}}} }} = \sqrt[3]{{\frac{V}{{2\pi }}}}\)

-- Mod Toán 12