Bài tập 1.65 trang 37 SBT Toán 12

Bài tập 1.65 trang 37 SBT Toán 12

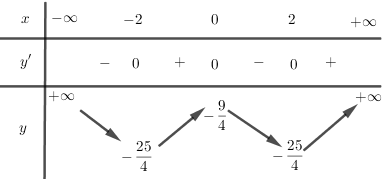
a) Tập xác định: D = R

Ta có 

\(y' = {x^3} - 4x;y\prime  = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x =  \pm 2
\end{array} \right.\)

Bảng biến thiên:

Đồ thị:

b) \(\begin{array}{l}
\frac{{{x^4}}}{4} - 2{x^2} - \frac{9}{4} = 0 \Leftrightarrow {x^4} - 8{x^2} - 9 = 0\\
 \Leftrightarrow ({x^2} + 1)({x^2} - 9) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - 3}\\
{x = 3}
\end{array}} \right.
\end{array}\)

Nên (C) cắt Ox tại hai điểm (−3;0) và (3;0).

Ta có: \(y' = {x^3} - 4x \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{y'\left( 3 \right) = 15}\\
{y'\left( { - 3} \right) =  - 15}
\end{array}} \right.\)

Phương trình tiếp tuyến của (C) tại điểm (3;0) là \(y = 15\left( {x - 3} \right) + 0\) 

hay \(y = 15x - 45\)

Phương trình tiếp tuyến của (C) tại điểm (−3;0) là \(y =  - 15\left( {x + 3} \right) + 0\) 

hay \(y =  - 15x - 45\).

Xét phương trình hoành độ giao điểm:

\(\frac{{{x^4}}}{4} - 2{x^2} - \frac{9}{4} = k - 2{x^2} \)

\(\Leftrightarrow {x^4} = 9 + 4k\,\,\left( * \right)\)

+) Nếu \(9 + 4k > 0 \Leftrightarrow k >  - \frac{9}{4}\) thì :

\(\begin{array}{l}
\left( * \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x^2} = \sqrt {9 + 4k} }\\
{{x^2} =  - \sqrt {9 + 4k} \left( L \right)}
\end{array}} \right.\\
 \Leftrightarrow x =  \pm \sqrt[4]{{9 + 4k}}
\end{array}\)

hay (∗) có hai nghiệm phân biệt.

+) Nếu \(9 + 4k = 0 \Leftrightarrow k =  - \frac{9}{4}\) thì:

\(\left(  *  \right) \Leftrightarrow {x^4} = 0 \Leftrightarrow x = 0\) 

hay (∗) có nghiệm duy nhất.

+) Nếu \(9 + 4k < 0 \Leftrightarrow k <  - \frac{9}{4}\) thì (∗) vô nghiệm.

Vậy: +) \(k =  - \frac{9}{4}\) : (C) và (P) có một điểm chung là \(\left( {0; - \frac{9}{4}} \right)\)

+) \(k >  - \frac{9}{4}\):  (C) và (P) có hai giao điểm.

+) \(k <  - \frac{9}{4}\)${\displaystyle \frac{\mathrm{}}{}}$ : (C) và (P) không cắt nhau.

-- Mod Toán 12