Bài tập 2 trang 45 SGK Giải tích 12

Bài tập 2 trang 45 SGK Giải tích 12

Các cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:

Quy tắc 1:

- Tìm tập xác định.

- Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.

- Lập bảng biến thiên.

- Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

- Tìm tập xác định.

- Tính \(f'(x)\). Tìm các nghiệm \({x_i}\) của phương trình \(f'(x)=0\).

- Tính \(f''(x)\) và \(f''(x_i)\) suy ra tính chất cực trị của các điểm \({x_i}\).

Chú ý: Nếu \(f''(x_i)=0\) thì ta phải dùng quy tắc 1 để xét cực trị tại \({x_i}\).

Tìm cực trị của hàm số \(y=x^4-2x^2+2\)

Xét hàm số: \(y=x^4-2x^2+2\)

Tập xác định: D = R

\(y'=4x^3-4x,y'=0\Leftrightarrow 4x^3-4x=0\)

\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=0\\ x=1 \end{matrix}\)

Xét dấy y':

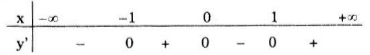
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại y_CĐ = y(0) = 2; đạt cực tiểu tại x = -1 và x = 1, giá trị cực tiểu y_CT = y(\(\pm\)1) =1.

-- Mod Toán 12