Bài tập 1.78 trang 40 SBT Toán 12

Bài tập 1.78 trang 40 SBT Toán 12

a) TXĐ: D = R.

Sự biến thiên: \(y' = 3{x^2} - 6x = 3x(x - 2);\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2
\end{array} \right.\)

Hàm số đồng biến trên mỗi khoảng \(( - \infty ;0),(2; + \infty )\)

Hàm số nghịch biến trên khoảng (0;2).

Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = y\left( 0 \right) = 0\)

Hàm số đạt cực tiểu tại \(x = 2;{y_{CT}} = y\left( 2 \right) =  - 4\)

Giới hạn: \(\mathop {\lim }\limits_{x \to  \pm \infty } y =  \pm \infty \)

Điểm uốn: \(y'' = 6x - 6,y'' = 0 \Leftrightarrow x = 1;\)

\(y\left( 1 \right) =  - 2\) suy ra đồ thị có điểm uốn I(1;−2).

Bảng biến thiên:

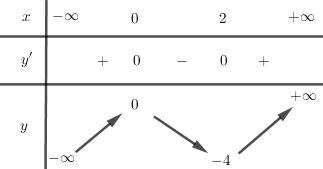
Đồ thị:

Ta có: \({x^3} - 3{x^2} - m = 0 \Leftrightarrow {x^3} - 3{x^2} = m\)

Phương trình (*) có 3 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt (C) tại 3 điểm phân biệt. Từ đó suy ra −4 < m < 0.

-- Mod Toán 12