Bài tập 75 trang 62 SGK Toán 12 NC

Bài tập 75 trang 62 SGK Toán 12 NC

a) Với m = 2 hàm số đã cho có dạng: y = x4 − 3x2 + 3

Tập xác định: D = R

\(\begin{array}{l}
y\prime  = 4{x^3} - 6x\\
y\prime  = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \frac{{\sqrt 6 }}{2}\\
x =  - \frac{{\sqrt 6 }}{2}
\end{array} \right.
\end{array}\)

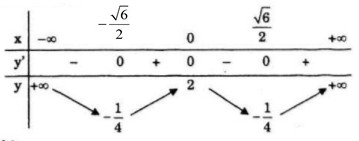
Hàm số đồng biến trên khoảng:

\(\left( { - \frac{{\sqrt 6 }}{2};0} \right),\left( {\frac{{\sqrt 6 }}{2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng:

\(\left( { - \infty ; - \frac{{\sqrt 6 }}{2}} \right),\left( {0;\frac{{\sqrt 6 }}{2}} \right)\)

Cực trị 

Hàm số đạt cực đại tại x = 0; y(0) = 2

Hàm số đạt cực tiểu tại:

\(x =  \pm \frac{{\sqrt 6 }}{2},y\left( { \pm \frac{{\sqrt 6 }}{2}} \right) =  - \frac{1}{4}\)

Giới hạn: \(\mathop {\lim}\limits_{x \to  \pm \infty } y =  + \infty \)

Bảng biến thiên:

Đồ thị:

Đồ thi cắt tung độ tại điểm (0; 2)

Đồ thị cắt hoành độ tại 4 điểm: \(( - \sqrt 2 ;0),( - 1;0),(1;0),(\sqrt 2 ;0)\)

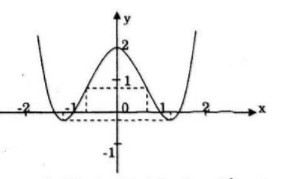
Đồ thị hàm số là hàm chẵn nhận trục Oy làm trục đối xứng.

b) Hoành độ giao điểm của đường cong (C) và trục là nghiệm phương trình

\(\begin{array}{l}
{x^4} - (m + 1){x^2} + m = 0\,\,(1)\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x^2} = 1}\\
{{x^2} = m}
\end{array}} \right.
\end{array}\)

(1) có 4 nghiệm phân biệt khi và chỉ khi m > 0 và m ≠ 1

Khi đó (1) có 4 nghiệm: 

\(x =  - 1;x = 1;x =  - \sqrt m ;x = \sqrt m \)

* \( - \sqrt m  <  - 1 < 1 < \sqrt m \)

(C) cắt trục tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(\sqrt m  - 1 = 1 - ( - 1) = 2 \Leftrightarrow m = 9\)

* \( - 1 <  - \sqrt m  < \sqrt m  < 1\)

(C) cắt trục hoành tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(1 - \sqrt m  = \sqrt m  - ( - \sqrt m ) = 2\sqrt m \)

Vậy m = 9 hoặc m = 1/9.

-- Mod Toán 12