Bài tập 1.75 trang 39 SBT Toán 12

Bài tập 1.75 trang 39 SBT Toán 12

a) Với m = 1 ta có hàm số \(y = 4{x^3} + x\)

TXĐ: D = R

Ta có: \(y' = 12{x^2} + 1 > 0,\forall x \in R\) nên hàm số đồng biến trên R và không có cực trị.

Bảng biến thiên:

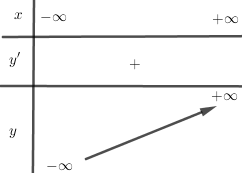
Đồ thị đi qua các điểm \(\left( {0;0} \right),\left( {1;5} \right),\left( { - 1; - 5} \right)\)

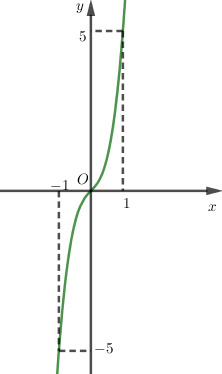
b) Do tiếp tuyến song song đường thẳng \(y = 13x + 1\)$\mathrm{}$ nên \(k = 13\)

Ta có: 

$\mathrm{}$\(12{x^2} + 1 = 13 \Leftrightarrow 12{x^2} = 12 \Leftrightarrow x =  \pm 1\)

+ Với x = 1 thì y = 5, ta có tiếp tuyến:

\(y = 13\left( {x - 1} \right) + 5\) hay \(y = 13x - 8\)

+ Với x = −1 thì y = −5, ta có tiếp tuyến:

\(y = 13\left( {x + 1} \right) - 5\) hay \(y = 13x + 8\)

Vậy có hai tiếp tuyến phải tìm là:

\(y = 13x \pm 8\).

c) Vì \(y' = 12{x^2} + m\) nên :

+) Với \(m \ge 0\) ta có \(y' \ge 0\) với mọi x.

Do đó hàm số (1) luôn luôn đồng biến khi \(m \ge 0\).

+) Với m < 0 thì \(y' = 0 \Leftrightarrow x =  \pm \sqrt {\frac{{ - m}}{{12}}} \)

Từ đó suy ra:

+) y′ > 0 với \(x <  - \sqrt {\frac{{ - m}}{{12}}} \) và \(x > \sqrt {\frac{{ - m}}{{12}}} \) 

nên hàm số đồng biến trên các khoảng:

\(\left( { - \infty ; - \sqrt {\frac{{ - m}}{{12}}} } \right),\left( {\sqrt {\frac{{ - m}}{{12}}} ; + \infty } \right)\)

+) y′ < 0 với \( - \sqrt { - \frac{m}{{12}}}  < x < \sqrt {\frac{{ - m}}{{12}}} \) nên hàm số nghịch biến trên khoảng:

\(\left( { - \sqrt {\frac{{ - m}}{{12}}} ;\sqrt {\frac{{ - m}}{{12}}} } \right)\)

-- Mod Toán 12