Bài tập 1.2 trang 7 SBT Toán 12
Bài tập 1.2 trang 7 SBT Toán 12
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) \({y = \frac{{3 - 2x}}{{x + 7}}}\);
b) \(y = \frac{1}{{{{(x - 5)}^2}}}\);
c) \(y = \frac{{2x}}{{{x^2} - 9}}\);
d) \(y = \frac{{{x^4} + 48}}{x}\);
e) \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\);
g) \(y = \frac{{{x^2} - 5x + 3}}{{x - 2}}\).
a) TXĐ: \ {-7}.
\(y' = \frac{{ - 17}}{{{{(x + 7)}^2}}}\)
trên các khoảng nên hàm số nghịch biến trên các khoảng đó.
b) TXĐ: \ {5}
\(y' = \frac{{ - 2}}{{{{(x - 5)}^3}}}\)
trên khoảng nên y nghịch biến trên khoảng .
trên khoảng nên y đồng biến trên khoảng .
c) TXĐ: \{-3;3}
\(y' = \frac{{ - 2({x^2} + 9)}}{{{{({x^2} - 9)}^2}}}\)
trên các khoảng nên hàm số nghịch biến trên các khoảng đó.
d) TXĐ: \{0}
\(\begin{array}{l}
y' = \frac{{3\left( {{x^4} - 16} \right)}}{{{x^2}}} = \frac{{3\left( {{x^2} - 4} \right)\left( {{x^2} + 4} \right)}}{{{x^2}}}\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 2\\
x = 2
\end{array} \right.
\end{array}\)
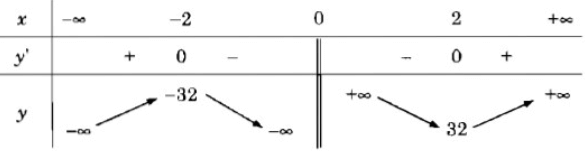
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng và nghịch biến trên các khoảng
e) TXĐ: \{-1}
\(\begin{array}{l}
y' = \frac{{{x^2} + 2x - 5}}{{{{\left( {x + 1} \right)}^2}}}\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 1 - \sqrt 6 \\
x = - 1 + \sqrt 6
\end{array} \right.
\end{array}\)
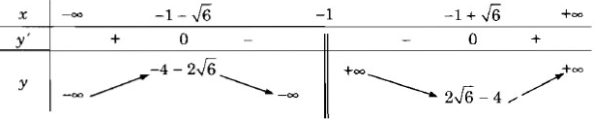
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6 ),( - 1 + \sqrt 6 ; + \infty )\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1),( - 1; - 1 + \sqrt 6 )\)
g) TXĐ: \{2}
\(y' = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\) (do \({x^2} - 4x + 7\) có \(\Delta ' = - 3 < 0\))
Vậy hàm số đã cho đồng biến trên các khoảng
-- Mod Toán 12
Copyright © 2021 HOCTAP247