Bài tập 6 trang 45 SGK Giải tích 12

Bài tập 6 trang 45 SGK Giải tích 12

Câu a:

Xét hàm số \(f(x)=-x^3+3x^2+9x+2\)

1) Tập xác định: D = R.

2) Sự biến thiên:

Chiều biến thiên: \(f'(x)=-3x^2+6x+9.\)

\(f'(x)=0\Leftrightarrow -3x^2+6x+9=0\)

\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=-1\\ x=3 \end{matrix}\)

Xét dấu f'(x):

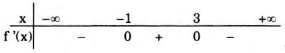
Vậy hàm số đồng biến trên khoảng (-1;3), nghịch biến trên khoảng \((-\infty ;-1)\) và \((3;+\infty )\).

Cực trị: Hàm số đạt cực đại tại x = 3 và giá trị cực đại y_CĐ = y(3) = 29, đạt cực tiểu tại x = - 1 và giá trị cực tiểu y_CT = y(-1) = -3.

Giới hạn:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  - \infty } y\\
 = \mathop {\lim }\limits_{x \to  - \infty } ( - {x^3} + 3{x^2} + 9x + 2)\\
 =  + \infty ,\\
\mathop {\lim }\limits_{x \to  + \infty } y\\
 = \mathop {\lim }\limits_{x \to  + \infty } ( - {x^3} + 3{x^2} + 9x + 2)\\
 =  - \infty 
\end{array}\)

Bảng biến thiên:

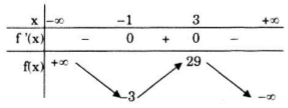
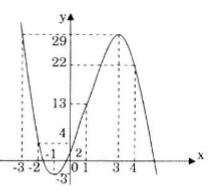
3) Đồ thị:

Ta có: y'' = - 6x + 6, y'' = 0 ⇔ x = 1. Vậy đồ thị hàm số nhận điểm (1;13) làm tâm đối xứng.

Đồ thị hàm số cắt Ox tại điểm (0;2).

Với \(x=-2\Rightarrow y=4\)

\(x=4\Rightarrow y=22\)

\(x=-3\Rightarrow y=29\)

Câu b:

Ta có: \(f'(x)=-3x^2+6x+9\)

\(\Rightarrow f '(x-1)\)

\(=-3(x-1)^2+6(x-1)+9\)

\(=-3(x^2-2x+1)+6x-6+9\)

\(=-3x^2+6x-3+6x-6+9\)

\(=-3x^2+12x\)

Do đó: \(f'(x-1)> 0\Leftrightarrow -3x^2+12x>0\)

\( \Leftrightarrow 0 < x < 4\)

Câu c:

Ta có: \(f''(x_0)=-6x_0+6\)

\(\Rightarrow f''(x_0)=-6\Leftrightarrow -6x_0+6=-6\)

\(\Leftrightarrow x_0=2\)

\(\Rightarrow f(x_0)=24\) và \(f'(x_0)=f'(2)=9\)

Vậy tiếp tuyến của đồ thị tại điểm x₀ theo yêu cầu bài toán là:

\(y=9(x-2)+24\Leftrightarrow y=9x+6\).

-- Mod Toán 12