Bài tập 73 trang 62 SGK Toán 12 NC

Bài tập 73 trang 62 SGK Toán 12 NC

a) Ta có: \(f'\left( x \right) = 3{x^2} + p\)

\(f\prime (x) = 0 \Leftrightarrow 3{x^2} + p = 0(1)\)

Hàm số f có một cực đại và một cực tiểu khi và chỉ khi khi phương trình (1) có hai nghiệm phân biệt ⇔p < 0

Khi đó hai nghiệm của (1) là: 

\(x =  - \sqrt { - \frac{p}{3}} ; x = \sqrt { - \frac{p}{3}} \)

Bảng biến thiên

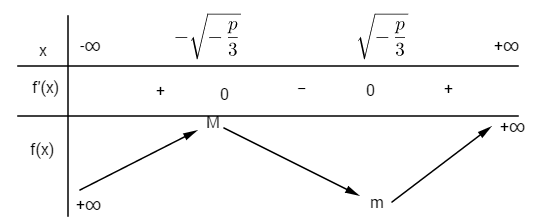
\(\begin{array}{l}
M = {\sqrt { - \left( { - \frac{p}{3}} \right)} ^3} - p\sqrt { - \frac{p}{3}}  + q\\
 = q - \frac{2}{3}p\sqrt { - \frac{p}{3}} 
\end{array}\)

\(\begin{array}{l}
m = {\sqrt { - \left( { - \frac{p}{3}} \right)} ^3} + p\sqrt { - \frac{p}{3}}  + q\\
 = q + \frac{2}{3}p\sqrt { - \frac{p}{3}} 
\end{array}\)

b) Nếu Mm < 0 và m < 0, khi đó, phương trình f(x) = 0 có ba nghiệm α, β, γ với 

\(\alpha  <  - \sqrt { - \frac{p}{3}} ; - \sqrt { - \frac{p}{3}}  < \beta  < \sqrt { - \frac{p}{3}} \)

Và \(\gamma  > \sqrt { - \frac{p}{3}} \)

c) Nếu Mm > 0 thì hai số M và m cùng dấu.

+ Nếu M < 0 và m < 0 thì phương trình (1) có nghiệm duy nhất (Lớn hơn \(\sqrt { - \frac{p}{3}} \))

+ Nếu M > 0 và m > 0 thì phương trình (1) có nghiệm duy nhất ( Nhỏ hơn \(\sqrt { - \frac{p}{3}} \))

Vậy điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: 

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{p < 0}\\
{Mm = {q^2} - \frac{4}{9}{p^2}\left( { - \frac{p}{3}} \right) < 0}
\end{array}} \right.\\
 \Leftrightarrow 4{p^3} + 27{q^2} < 0
\end{array}\)

-- Mod Toán 12