Bài tập 79 trang 62 SGK Toán 12 NC

Bài tập 79 trang 62 SGK Toán 12 NC

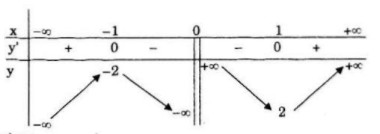
a) Tập xác định: D = R∖{0}

\(\begin{array}{l}
y\prime  = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\\
y\prime  = 0 \Leftrightarrow x =  \pm 1
\end{array}\)

Hàm số đồng biến trên khoảng: \(( - \infty ; - 1);(1; + \infty )\)

Hàm số nghịch biến trên khoảng: (−1; 0); (0; 1)

+) Cực trị:

 Hàm số đạt cực đại tại: x = −1; y(−1) = −2

Hàm số đạt cực tiểu tại: x = 1; y(1) = 2

+) Giới hạn:

\(\mathop {\lim y}\limits_{x \to {0^ - }}  =  - \infty ;\mathop {\lim y}\limits_{x \to {0^ + }}  =  + \infty \)

Tiệm cận đứng: x = 0

\(\begin{array}{l}
\mathop {\lim}\limits_{x \to  \pm \infty } y =  \pm \infty \\
\mathop {\lim}\limits_{x \to \infty } (y - x) = \mathop {\lim}\limits_{x \to \infty } \frac{1}{x} = 0
\end{array}\)

Tiệm cận xiên: y = x

Bảng biến thiên:

Đồ thị:

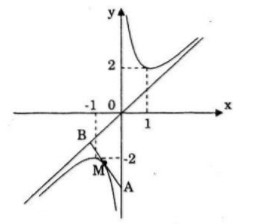
b) Tiệm cận đứng x = 0; Tiệm cận xiên y = x.
Ta có \(f(x) = 1 - \frac{1}{{{x^2}}}\).

Phương trình tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\) là:

\(y = \left( {1 - \frac{1}{{x_0^2}}} \right)(x - {x_0}) + {x_0} + \frac{1}{{{x_0}}}\)

Thay x = 0 vào phương trình trên, ta được tung độ của điểm A:

\({y_A} = \left( {1 - \frac{1}{{x_0^2}}} \right)\left( { - {x_0}} \right) + {x_0} + \frac{1}{{{x_0}}} = \frac{2}{{{x_0}}}\) 

Vậy \(A\left( {0;\frac{2}{{{x_0}}}} \right)\)

Hoành độ của điểm B là nghiệm của phương trình

\(\begin{array}{l}
\left( {1 - \frac{1}{{x_0^2}}} \right)(x - {x_0}) + {x_0} + \frac{1}{{{x_0}}} = x\\
 \Leftrightarrow  - \frac{x}{{{x_0}}} + \frac{2}{{{x_0}}} = 0 \Leftrightarrow x = 2{x_0}
\end{array}\)

x_B = 2x₀. Vậy B(2x₀; 2x₀)

Ta có: \({x_M} = {x_0} = \frac{{0 + 2{x_0}}}{2} = \frac{{{x_A} + {x_B}}}{2}\)

Vì ba điểm A, M, B thẳng hàng nên từ đó suy ra rằng M là trung điểm của đoạn thẳng AB.

Diện tích tam giác OAB là:

\(\begin{array}{l}
S = \frac{1}{2}\left| {{y_A}} \right|.\left| {{y_B}} \right|\\
 = \frac{1}{2}\left| {\frac{2}{{{x_0}}}} \right|.\left| {2{x_0}} \right| = 2,\forall {x_0} \ne 0
\end{array}\)

-- Mod Toán 12