Bài tập 5 trang 18 SGK Giải tích 12

Bài tập 5 trang 18 SGK Giải tích 12

Phân tích đề & Phương pháp giải:

Đây là bài toán tìm tham số để hàm số có cực trị thỏa mãn điều kiện cho trước.

Với dữ kiện của đề bài, ta nhận định:

- Nếu a = 0, hàm số đã cho sẽ trở thành hàm số bậc nhất và không có cực trị.

- Nếu a khác 0, hàm số đã cho là một hàm số bậc ba, ta áp dụng quy tắc 1 để tìm tham số a và b theo yêu cầu bài toán.

Lời giải:

Khai thác dữ kiện đề bài cho ta có lời giải chi tiết bài 5 như sau:

- Với a = 0 hàm số trở thành y = - 9x+b không có cực trị.

- Với \(a \ne 0\) ta có: \(y' = 5{a^2}{x^2} + 4ax - 9\)

\(y' = 0 \Leftrightarrow 5{a^2}{x^2} + 4ax - 9 \Leftrightarrow \left[ \begin{array}{l} x = - \frac{9}{{5a}}\\ x = \frac{1}{a} \end{array} \right.\)

+ Với a < 0 ta có bảng biến thiên:

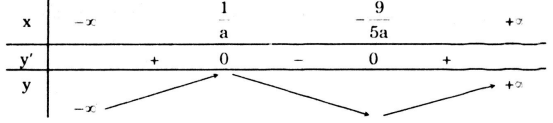
Theo giả thiết \({x_0} =  - \frac{5}{9}\) là điểm cực đại nên \(\frac{1}{a}=-\frac{5}{9}\Leftrightarrow a=-\frac{9}{5}.\) 

Giá trị cực tiểu là số dương nên:

\(y_{CT}=y\left ( -\frac{9}{5a} \right )=y(1)>0\)

\(\Leftrightarrow \frac{5}{3}\cdot \left ( -\frac{9}{5} \right )^{2}+2\cdot \left ( -\frac{9}{5} \right )-9+b>0\)

\(\Leftrightarrow b>\frac{36}{5}.\)

+ Với a < 0 ta có bảng biến thiên:

Vì \({x_0} =  - \frac{5}{9}\) là điểm cực đại nên \( - \frac{9}{{5a}} =  - \frac{5}{9} \Leftrightarrow a = \frac{{81}}{{25}}\). 

Giá trị cực tiểu là số dương nên:

\({y_{CT}} = y\left( {\frac{1}{a}} \right) = \frac{5}{{3a}} + \frac{2}{a} - \frac{9}{a} + b > 0\)\(\small \Leftrightarrow b>\frac{400}{243}.\)

Vậy các giá trị a, b cần tìm là: 

\(\left\{ \begin{array}{l}
a =  - \frac{9}{5}\\
b > \frac{{36}}{5}
\end{array} \right. \vee \left\{ \begin{array}{l}
a = \frac{{81}}{{25}}\\
b > \frac{{400}}{{243}}
\end{array} \right.\)

-- Mod Toán 12