Bài tập 10 trang 46 SGK Giải tích 12
Bài tập 10 trang 46 SGK Giải tích 12
Cho hàm số \(y=-{{x}^{4}}+2m{{x}^{2}}-2m+1\) với (m tham số) có đồ thị \(\left( {{C}_{m}} \right)\).
a) Biện luận theo m số cực trị của hàm số.
b) Với giá trị nào của m thì \(\left( {{C}_{m}} \right)\) cắt trục hoành?
c) Xác định m để \(\left( {{C}_{m}} \right)\) có cực đại, cực tiểu.
Câu a:
y= - x4 + 2mx2 - 2m + 1
Tập xác định: D = R
y'= - 4x3 + 4mx = - 4x (x2 - m)
y' = 0 ⇔ - 4x (x2 - m) = 0 \(\Leftrightarrow \bigg \lbrack \begin{matrix} x=0\\ x^2-m=0 \end{matrix}\)
+ Nếu \(m\leq 0\) thì \(x^2-m\geq 0\).
Ta có bảng xét dấu y':
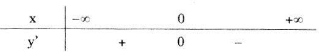
⇒ Hàm số có một điểm cực đại là x = 0.
+ Nếu m > 0 thì :
\(x^2-m=0 \Leftrightarrow \bigg \lbrack \begin{matrix} x=-\sqrt{m}\\ x=\sqrt{m} \end{matrix}\).
Ta có bảng xét dấu y':
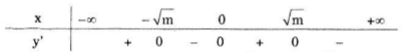
⇒ Hàm số có hai điểm cực đại là \(x=-\sqrt{m}\) và \(x=\sqrt{m}\), hàm số có một điểm cực tiểu là x = 0.
Vậy với \(m\leq 0\) thì hàm số có một cực trị.
Với m > 0 thì hàm số có ba cực trị.
Câu b:
Xét hàm số y = f(x) = -x4 + 2mx2 - 2m + 1.
Ta có: \(f(\pm 1)=0 \ \forall m\)
⇒ đồ thị cắt Ox tại ít nhất 2 điểm.
Vậy mới mọi m thì đồ thị luôn cắt trục hoành.
Câu c:
Từ câu a ta có đồ thị có cực đại, cực tiểu khi m > 0.
-- Mod Toán 12
Copyright © 2021 HOCTAP247
