Bài tập 1.81 trang 41 SBT Toán 12

Bài tập 1.81 trang 41 SBT Toán 12

a) TXĐ: D = R∖{2}

Có \(y' = \frac{{ - 9}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \ne 2\) nên hàm số nghịch biến trên các khoảng (−∞;2) và (2;+∞) và không có cực trị.

TCĐ: x = 2 và TCN y = 3

Bảng biến thiên:

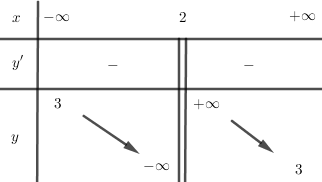
Đồ thị:

b) Phương trình đường thẳng đi qua gốc tọa độ O có dạng y = kx.

Để xác định tọa độ tiếp điểm của hai đường: y = 3(x+1)x−2 và y = kx, ta giải hệ:

\(\left\{ {\begin{array}{*{20}{l}}
{\frac{{3(x + 1)}}{{x - 2}} = kx}\\
{ - \frac{9}{{{{(x - 2)}^2}}} = k}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{{3(x + 1)}}{{x - 2}} + \frac{9}{{{{(x - 2)}^2}}} = 0}\\
{ - \frac{9}{{{{(x - 2)}^2}}} = k}
\end{array}} \right.\)

Giải phương trình thứ nhất ta được: \(x =  - 1 \pm \sqrt 3 \)

Thay vào phương trình thứ hai ta có: \({k_1} =  - \frac{3}{2}(2 + \sqrt 3 );{k_2} =  - \frac{3}{2}(2 - \sqrt 3 )\)

Từ đó có hai phương trình tiếp tuyến là: 

\(y =  - \frac{3}{2}(2 + \sqrt 3 )x\); 

\(y =  - \frac{3}{2}(2 - \sqrt 3 )x\)

c) Ta có: \(y = \frac{{3(x + 1)}}{{x - 2}} \Rightarrow y = 3 + \frac{9}{{x - 2}}\)

Để M(x,y) ∈ (C) có tọa độ nguyên thì:

\(\begin{array}{l}
x \in Z\\
\frac{9}{{x - 2}} \in Z\\
 \Rightarrow (x - 2) \in U(9) = \{  \pm 1; \pm 3; \pm 9\} \\
 \Rightarrow x \in \left\{ {1;3; - 1;5; - 7;11} \right\}
\end{array}\)

Do đó, ta có 6 điểm trên (C) có tọa độ nguyên là: (1;−6), (3;12), (−1;0)$,$ (5;6), (−7;2), (11;4).

-- Mod Toán 12