Bài tập 9 trang 44 SGK Giải tích 12

Bài tập 9 trang 44 SGK Giải tích 12

Câu a:

Đồ thị hàm số đi qua điểm (0;-1) nên ta có: 

\( - 1 = \frac{{\left( {m + 1} \right).0 - 2m + 1}}{{0 - 1}} \Leftrightarrow m = 0\)

Câu b:

Với m = 0 ta có hàm số \(y = \frac{{x + 1}}{{x - 1}}\)

Tập xác định: \(D = \mathbb{R}\backslash {\rm{\{ }}1\} .\)

Giới hạn và tiệm cận:

\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty ;\)

\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty\) 

Nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1;\)

\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1\)

Nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Sự biến thiên:

Đạo hàm: \(y' = - \frac{2}{{{{(x - 1)}^2}}} < 0,\forall x \ne 1.\)

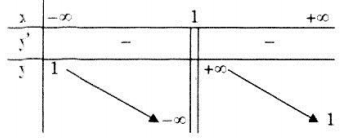
Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng: \(\left( { - \infty ;1} \right);\,\,\left( {1; + \infty } \right).\)

Hàm số không có cực trị.

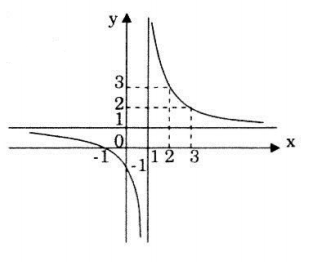
Đồ thị:

Đồ thị hàm số nhận điểm I(1;1) làm tâm đối xứng.

Đồ thị cắt trục Ox tại điểm (-1;0), cắt Oy tại điểm (0;-1).

Với x = 2 suy ra y = 3.

Với x = 3 suy ra y = 2.

Đồ thị của hàm số:

Câu c:

Đồ thị hàm số cắt trục tung tại điểm M(0;1). 

Ta có: \(y' =  - \frac{2}{{{{\left( {x - 1} \right)}^2}}}\) suy ra: y'(0) = - 2.

Phương trình tiếp tuyến của tại M là: y - (-1) = y'(0)(x - 0) ⇔ y = - 2x - 1.

-- Mod Toán 12