Bài tập 5 trang 45 SGK Giải tích 12

Bài tập 5 trang 45 SGK Giải tích 12

Câu a:

Với m = 1. Ta có hàm số: y = 2x² + 2x

1) Tập xác định: R

2) Sự biến thiên:

Chiều biến thiên: 

\(y'=4x+2,\)

\(y'=0\Leftrightarrow 4x+2=0\Leftrightarrow x=-\frac{1}{2}\)

Xét dấu y':

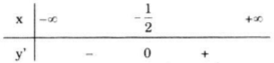
Vậy hàm số đồng biến trên khoảng \(\left ( -\frac{1}{2} ;+\infty \right )\), nghịch biến trên khoảng \(\left ( -\infty ;-\frac{1}{2} \right )\).

Cực trị: Hàm số đạt cực tiểu tại \(x=-\frac{1}{2}\), giá trị cực tiểu \(y_{CT}=y\left ( -\frac{1}{2} \right )=-\frac{1}{2}\). Hàm số không có cực đại.

Giới hạn:

\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }(2x^2+2x)=+\infty,\)

\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }(2x^2+2x)=+\infty\)

Bảng biến thiên:

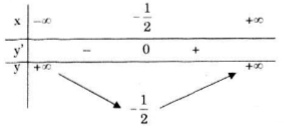
3) Đồ thị:

Đồ thị cắt Ox tại các điểm (0;0) và (-1;0), cắt Oy tại điểm (0;0).

\(x=-2\Rightarrow y=4\)

\(x=1\Rightarrow y=4\)

Câu b:

Xét hàm số y = 2x² + 2mx + m-1

\(y'=4x+2m,\)

\(y'=0\Leftrightarrow 4x+2m=0\Leftrightarrow x=-\frac{m}{2}\)

Bảng biến thiên:

Từ bảng biến thiên ta suy ra:

i) Hàm số đồng biến trên khoảng \((-1;+\infty )\) khi \(-\frac{m}{2}\leq -1\Leftrightarrow m\geq 2\).

ii) Hàm số có cực trị trên khoảng \((-1;+\infty )\) khi \(-\frac{m}{2}> -1\Leftrightarrow m< 2\).

Câu c:

Phương trình hoành độ giao điểm của (C_m) với trục hoành:

\(2{x^2} + 2mx + m - 1 = 0\)

Ta có: 

\(\Delta ' = {m^2} - 2m + 2 \)

\(= {(m - 1)^2} + 1 > 0,\forall m \in \mathbb{R}.\)

Vậy: (Cm) luôn cắt trục hoành tại hai điểm phân biệt.

-- Mod Toán 12