Bài tập 3.9 trang 103 SBT Hình học 12

Bài tập 3.9 trang 103 SBT Hình học 12

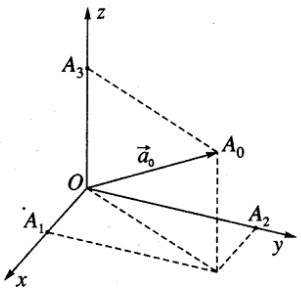
Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng  với vecto \(\vec a\) , ta có \(\overrightarrow {{a_0}}  = \frac{1}{{|\vec a|}}\vec a\)

Gọi \(\overrightarrow {O{A_0}}  = \overrightarrow {{a_0}} \) và các điểm A₁, A₂, A₃ theo thứ tự là hình chiếu vuông góc của điểm A₀ trên các trục Ox, Oy, Oz.

Khi đó ta có: \(\frac{{|\overrightarrow {O{A_1}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \alpha ,\frac{{|\overrightarrow {O{A_2}} |}}{{|\overrightarrow {O{A_0}|} }} = \cos \beta ,\frac{{|\overrightarrow {O{A_3}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \gamma \)

Vì \(|\overrightarrow {O{A_0}} | = 1\) nên \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)

Ta có \(\overrightarrow {O{A_0}}  = \overrightarrow {O{A_1}}  + \overrightarrow {O{B_2}}  + \overrightarrow {O{A_3}} \) ta suy ra: \(\overrightarrow {O{A_0}}  = \cos \alpha \vec i + \cos \beta \vec j + \cos \gamma \vec k\) hay \(\overrightarrow {O{A_0}}  = (\cos \alpha ;\cos \beta ;\cos \gamma )\)

Vì \(\overrightarrow {O{A_0}}  = \overrightarrow {{a_0}} \) mà \(\left| {\overrightarrow {{a_0}} } \right| = 1\) nên ta có: \({\cos ^2}\alpha  + {\cos ^2}\beta  + {\cos ^2}\gamma  = 1\)

-- Mod Toán 12