Bài tập 12 trang 82 SGK Hình học 12 NC

Bài tập 12 trang 82 SGK Hình học 12 NC

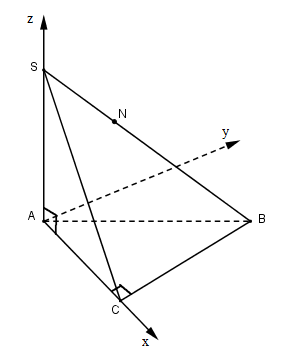
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.

Ta có: A = (0; 0; 0), C = (b; 0; 0), B = (b; a; 0), S = (0; 0; h).

\(M\left( {\frac{b}{2};0;0} \right),\overrightarrow {SB}  = (b;a; - h)\)

Gọi N(x; y; z) thì \(\overrightarrow {SN}  = \left( {x;y;z - h} \right)\)

\(\begin{array}{l}
\overrightarrow {SN}  = \frac{1}{3}\overrightarrow {SB}  \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{b}{3}}\\
{y = \frac{a}{3}}\\
{z - h = \frac{{ - h}}{3}}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{b}{3}}\\
{y = \frac{a}{3}}\\
{z = \frac{{2h}}{3}}
\end{array}} \right. \Rightarrow N\left( {\frac{b}{3};\frac{a}{3};\frac{{2h}}{3}} \right)
\end{array}\)

a)

\(\begin{array}{*{20}{l}}
{\overrightarrow {MN}  = \left( {\frac{b}{3} - \frac{b}{2};\frac{a}{3};\frac{{2h}}{3}} \right) = \left( { - \frac{b}{6};\frac{a}{3};\frac{{2h}}{3}} \right)}\\
\begin{array}{l}
MN = \sqrt {\frac{{{b^2}}}{{36}} + \frac{{{a^2}}}{9} + \frac{{4{h^2}}}{9}} \\
 = \frac{1}{6}\sqrt {{b^2} + 4{a^2} + 16{h^2}} 
\end{array}
\end{array}\)

b)

\(\begin{array}{l}
MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB}  = 0\\
 \Leftrightarrow  - \frac{{{b^2}}}{6} + \frac{{{a^2}}}{3} + \frac{{ - 2{h^2}}}{3} = 0\\
 \Leftrightarrow 4{h^2} = 2{a^2} - {b^2}
\end{array}\)

-- Mod Toán 12