Bài tập 3 trang 99 SGK Hình học 12
Bài tập 3 trang 99 SGK Hình học 12
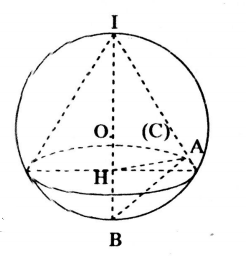
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.
a) Tính thể tích của hình nón theo r và h.
b) Xác định h để thể tích của hình nón là lớn nhất.
Câu a:
Gọi H là tâm đường tròn (C), IB là đường kính mặt cầu.
Suy ra: \(H,O \in IB\)
Lấy A là 1 điểm trên (C).
Ta có tam giác IHA đồng dạng với tam giác IAB.
Suy ra: \(\frac{IH}{IA}=\frac{IA}{IB}\Rightarrow IA^2=IH.IB=h.2r=2rh.\)
Mặc khác:
\(\begin{array}{l} I{A^2} = I{H^2} + H{A^2}\\ \Rightarrow H{A^2} = I{A^2} - I{H^2} = 2rh - {h^2} = h(2r - h). \end{array}\)
Vậy đường tròn (C) có bán kính là: \(R = \sqrt {h(2r - h)} .\)
Thể tích của khối nón là: \(V = \frac{1}{3}\pi .{R^2}.h = \frac{1}{3}.\pi .h(2R - h).h = \frac{1}{3}.\pi (2r - h){h^2}.\)
Câu b:
Xét hàm số \(V(h) = \left( {2r - h} \right).{h^2}\) với \(0<h<2r.\)
Ta có:
\(\begin{array}{l} V'(h) = - 3{h^2} + 4rh = h( - 3h + 4r)\\ V'(h) = 0 \Leftrightarrow \left[ \begin{array}{l} h = 0 \notin \left( {0;2r} \right)\\ h = \frac{{4r}}{3} \in \left( {0;2r} \right) \end{array} \right. \end{array}\)
Bảng biến thiên:
Vậy thể tích khối nón lớn nhất là \(V=\frac{{32}}{{81}}{r^3}\) khi \(h = \frac{4}{3}r.\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247

.PNG)