Bài tập 10 trang 91 SGK Hình học 12

Bài tập 10 trang 91 SGK Hình học 12

Phương pháp:

Từ dữ kiện đề bài, ta chọn một đỉnh bất kì của hình lập phương là gốc tọa độ. Khi đó, 3 cạnh của hình lập phương đi qua đỉnh đó chính là phương của các trục Ox, Oy, Oz.

Sau khi xây dựng xong hệ trục tọa độ, ta xác định tọa độ các đỉnh lúc này và tiến hành giải bài toán bằng phương pháp tọa độ trong không gian.

Lời giải:

Ta có lời giải chi tiết bài 10 như sau:

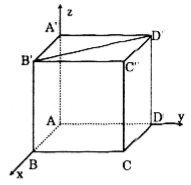
Ta chọn hệ toạ độ Oxyz sao cho \(O\equiv A, \vec{i}=\overrightarrow{AB},\vec{j}=\overrightarrow{AD}, \vec{k}=\overrightarrow{AA'}\)

Trong hệ toạ độ Oxyz ta có: A'(0;0;1), B(1;0;0), D(0;1;0), B'(1;0;1), D'(0;1;1), C(1;1;0).

Đặt \((\alpha )=(A'BD)\) và \((\beta )=(B'D'C')\).

Mặt phẳng \(\left ( \alpha \right )\) đi qua B(1;0;0), D(0;1;0), A'(0;0;1). Nên ta có phương trình theo đoạn chắn của \(\left ( \alpha \right )\) là:

\((\alpha ):\frac{x}{1}+\frac{y}{1}+\frac{z}{1}=1\) suy ra \(x+y+z-1=0.\)

Ta có: 

\(\begin{array}{l} \overrightarrow {B'D'} = \left( { - 1;1;0} \right)\\ \overrightarrow {B'C} = (0;1; - 1)\\ \Rightarrow \left[ {\overrightarrow {B'D'} ;\overrightarrow {B'C} } \right] = \left( {\left| {\begin{array}{*{20}{c}} 1&0\\ 1&{ - 1} \end{array}} \right|;\left| {\begin{array}{*{20}{c}} 0&{ - 1}\\ { - 1}&0 \end{array}} \right|;\left| {\begin{array}{*{20}{c}} { - 1}&1\\ 0&1 \end{array}} \right|} \right) = \left( { - 1; - 1; - 1} \right) \end{array}\)

Mặt phẳng \(\left ( \beta \right )\) đi qua B'(1;0;1) và nhận vectơ \(\overrightarrow n = \left[ {\overrightarrow {B'D'} ;\overrightarrow {B'C} } \right]\) làm một vectơ pháp tuyến, nên có phương trình là:

\((\beta ):(x-1)+(y-1)+z=0\Leftrightarrow x+y+z-2=0\).

Vậy ta có:

\(d(A,(\alpha ))=\frac{\left | -1 \right |}{\sqrt{1^2+1^2+1^2}}=\frac{1}{\sqrt{3}}\).

\(d(A,(\beta ))=\frac{\left | -2 \right |}{\sqrt{1^2+1^2+1^2}}=\frac{2}{\sqrt{3}}\).

-- Mod Toán 12