Bài tập 5 trang 80 SGK Hình học 12

Bài tập 5 trang 80 SGK Hình học 12

Phương pháp:

Mặt phẳng đi qua 3 điểm A, B, C không thẳng hàng có một VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\).

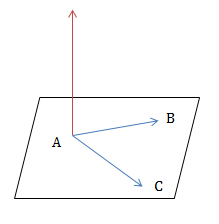
Giả sử mặt phẳng (P), có cặp VTCP là \(\vec u_1\) và \(\vec u_2\) thì \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\) là một VTPT của mặt phẳng (P).

Lời giải:

Ta có lời giải chi tiết câu a, b bài 5 như sau:

Câu a:

Ta có \(\overrightarrow{AC}=(0;-1;1); \overrightarrow{AD}=(-1;-1;3)\)

Mặt phẳng (ACD) có vecto pháp tuyến \(\vec{n}=\left [ \overrightarrow{AC}, \overrightarrow{AD} \right ]= (-2;-1;-1)\)

Vậy phương trình của mặt phẳng (ACD) là:

\(-2(x-5)-1(y-1)-1(z-3)=0\Leftrightarrow 2x+y+z-14=0\)

Câu b:

Ta có: \(\overrightarrow{AB}=(-4;5;-1); \overrightarrow{CD}=(-1;0;2)\).

Suy ra mặt phẳng \((\alpha )\) đi qua AB và song song với CD nên có một vectơ pháp tuyến là \(\vec{n}=\left [ \overrightarrow{AB}, \overrightarrow{CD} \right ]=(10;9;5)\).

Vậy phương trình của mặt phẳng \((\alpha )\) là:

\(10(x-5)+9(y-1)+5(z-3)=0\Leftrightarrow 10x+9y+5z-74=0\).

-- Mod Toán 12

Video hướng dẫn giải bài 5 SGK