Bài tập 3 trang 68 SGK Hình học 12
Bài tập 3 trang 68 SGK Hình học 12
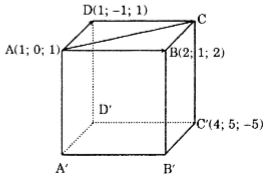
Cho hình hộp ABCD.A'B'C'D' biết A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1), C'=(4; 5; -5). Tính tọa độ các đỉnh còn lại của hình hộp.
Phương pháp:
Dựa vào tính chất của hình hộp, xác định các vectơ bằng nhau và áp dụng tính chất :\(\vec{u}=u'\Leftrightarrow \left\{\begin{matrix} x=x'\\ y=y'\\ z=z' \end{matrix}\right.\)
Lời giải:
Ta có lời giải chi tiết bài 3 như sau:
Ta có:
\(\overrightarrow{AB}=(1;1;1)\)
\(\overrightarrow{AD}=(0;-1;0)\)
\(\overrightarrow{BC}=\overrightarrow{AD}\Leftrightarrow \left\{\begin{matrix} x_C-2=0\\ y_C-1=-1\\ z_C-2=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_C=2\\ y_C=0\\ z_C=2 \end{matrix}\right.\)
Vậy C=(2;0;2)
Suy ra \(\overrightarrow{CC'}=(2;5;-7)\)
Từ \(\overrightarrow{AA'}=\overrightarrow{BB'}= \overrightarrow{DD'}=\overrightarrow{CC'}=(2;5;-7)\)
\(\overrightarrow {AA'} = (2;5; - 7) \Rightarrow\) \(\left\{\begin{matrix} x_{A'}-1=2\\ y_{A'}-0=5\\ z_{A'}-1=-7 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{A'}=3\\ y_{A'}=5\\ z_{A'}=-6\\ \end{matrix}\right.\)
Vậy A'(3;5;-6).
\(\overrightarrow {BB'} = (2;5; - 7) \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{B'}} - 2 = 2}\\ {{y_{B'}} - 1 = 5}\\ {{z_{B'}} - 2 = - 7} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{B'}} = 4}\\ {{y_{B'}} = 6}\\ {{z_{B'}} = - 5} \end{array}} \right.\)
Vậy: B'(4;6;-5).
\(\overrightarrow {DD'} = (2;5; - 7) \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{D'}} - 1 = 2}\\ {{y_{D'}} + 1 = 5}\\ {{z_{D'}} - 1 = - 7} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{D'}} = 3}\\ {{y_{D'}} = 4}\\ {{z_{D'}} = - 6} \end{array}} \right.\)
D'=(3;4;-6).
-- Mod Toán 12
Video hướng dẫn giải bài 3 SGK
Copyright © 2021 HOCTAP247
