Bài tập 3.39 trang 130 SBT Hình học 12

Bài tập 3.39 trang 130 SBT Hình học 12

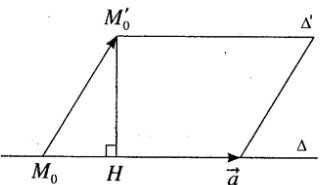
a)  Δ đi qua điểm M₀(1; -3; 4) và có vecto chỉ phương \(\vec a = (2;1; - 2)\)

Δ′ đi qua điểm M₀’ (-2; 1; -1) và có vecto chỉ phương \(\overrightarrow {a'}  = ( - 4; - 2;4)\)

Ta có \(\left\{ {\begin{array}{*{20}{c}}
{\overrightarrow {a'}  = 2\vec a}\\
{{M_0} \notin {\rm{\Delta '}}}
\end{array}} \right.\)

Vậy Δ′ song song với Δ.

b) Ta có \(\overrightarrow {{M_0}M_0^\prime }  = ( - 3;4; - 5)\)

           \(\vec a = (2;1; - 2)\)

\(\vec n = \overrightarrow {{M_0}M_0^\prime }  \wedge \vec a = ( - 3; - 16; - 11)\)

\(d({\rm{\Delta }},{\rm{\Delta '}}) = M_0^\prime H = \frac{{|\vec n|}}{{|\vec a|}} = \frac{{\sqrt {9 + 256 + 121} }}{{\sqrt {4 + 1 + 4} }} = \frac{{\sqrt {386} }}{3}\)

-- Mod Toán 12