Bài tập 5 trang 92 SGK Hình học 12

Bài tập 5 trang 92 SGK Hình học 12

Phương pháp:

Trước khi giải bài 5, ta ôn lại vị trí tương đối giữa mặt phẳng và mặt cầu đã học ở chương 2 Hình học 12:

Cho mặt cầu S(O;r) tâm O bán kính r và mặt phẳng (P); H là hình chiếu vuông góc của O lên mặt phẳng (P).

Khi đó h=OH là khoảng cách từ O đến mặt phẳng (P). 

• Nếu h=r thì (P) tiếp xúc mặt cầu.

Ghi nhớ: Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S(O;r) tại điểm H là (P) vuông góc với bán kính OH tại điểm H đó.

• Nếu h>r thì (P) không có điểm chung với mặt cầu.

• Nếu h < r thì (P) cắt mặt cầu S(O;r) theo giao tuyến là một đường tròn tâm H bán kính \(r' = \sqrt {{r^2} - {h^2}} .\)

​

Lời giải:

Lời giải chi tiết bài 5 như sau:

Mặt cầu (S) có tâm là I(3;-2;1) và có bán kính R = 10.

\(d(I,(\alpha ))=\frac{\left | 2.3+2.2-1+9 \right |}{\sqrt{2^2+2^2+1^2}}=6\)

Ta có: \(d(I,(\alpha ))=6< 10\), suy ra mặt phẳng \((\alpha )\) cắt (S) theo một đường tròn (C) chính là hình chiếu vuông góc của I trên mặt phẳng \((\alpha )\).

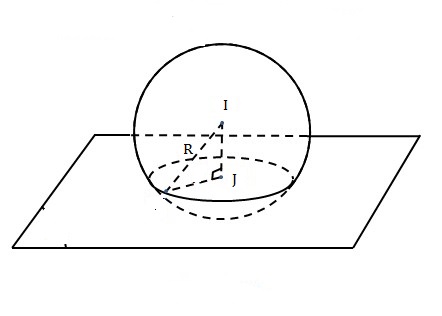
Mặt phẳng \((\alpha )\) có VTPT \(\overrightarrow n = \left( {2; - 2; - 1} \right)\).

Gọi \(\Delta\) là đường thẳng đi qua I(3;-2;1) và vuông góc với \((\alpha )\) suy ra \(\Delta\) nhận \(\overrightarrow n = \left( {2; - 2; - 1} \right)\) làm VTCP:

Vậy phương trình tham số của \(\Delta\) là: \(\left\{\begin{matrix} x=3+2t\\ y=-2-2t\\ z=1-t \end{matrix}\right.\)

\(\Delta\) cắt \((\alpha )\) tại J(3+2t; -2-2t; 1-t). Vì \(J\in (\alpha )\) nên ta có:

\(2(3+2t) -2(-2-2t) - (1-t)+9=0\Leftrightarrow 9t+18=0\Leftrightarrow t=-2\)

Vậy ta được J(-1; 2; 3)

Bán kính r của (C) được tính theo công thức:

\(r=\sqrt{R^2-d^2(I,(\alpha ))}=\sqrt{100-36}=8\)

Vậy đường tròn (C) có tâm J(-1; 2; 3) và bán kính r = 8.

-- Mod Toán 12