Bài tập 3.38 trang 130 SBT Hình học 12

Bài tập 3.38 trang 130 SBT Hình học 12

a) Gọi \((\alpha )\)$$ là mặt phẳng chứa Δ và song song với Δ′. Hai vecto có giá song song hoặc nằm trên \((\alpha )\)$$ là: \(\vec a = (1; - 1;0)\) và \({\vec a^\prime } = ( - 1;1;1)\). Suy ra \(\overrightarrow {{n_\alpha }}  = ( - 1; - 1;0)\)

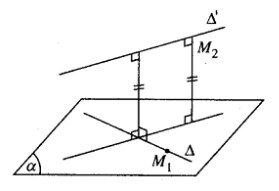
\((\alpha )\) đi qua điểm M₁(1; -1; 1) thuộc Δ và có vecto pháp tuyến: \(\overrightarrow {{n_{\alpha '}}}  = (1;1;0)\)

Vậy phưong trình của mặt phẳng \((\alpha )\)$$ có dạng  x – 1 + y + 1= 0 hay x + y = 0

Ta có:  M₂ (2; 2; 0) thuộc đường thẳng Δ′.

      \(d({\rm{\Delta }},{\rm{\Delta '}}) = d({M_2},(\alpha )) = \frac{{|2 + 2|}}{{\sqrt {1 + 1} }} = 2\sqrt 2 \)

b) Hai đường thẳng Δ và Δ′ có phương trình là:

\(\Delta :\left\{ \begin{array}{l}
x = t\\
y = 4 - t\\
z =  - 1 + 2t
\end{array} \right.\) và \({\rm{\Delta '}}:\left\{ {\begin{array}{*{20}{c}}
{x = t'}\\
{y = 2 - 3t'}\\
{z =  - 3t'}
\end{array}} \right.\)

Phương trình mặt phẳng \((\alpha )\) chứa Δ và song song với Δ′ là 9x + 5y – 2z – 22 = 0

Lấy điểm M’(0; 2; 0) trên Δ′.

Ta có \(d({\rm{\Delta }},{\rm{\Delta '}}) = d(M',(\alpha )) = \frac{{|5.(2) - 22|}}{{\sqrt {81 + 25 + 4} }} = \frac{{12}}{{\sqrt {110} }}\)

Vậy khoảng cách giữa hai đường thẳng Δ và  Δ′ là \(\frac{{12}}{{\sqrt {110} }}\).

-- Mod Toán 12