Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.44 trang 131 SBT Hình học 12
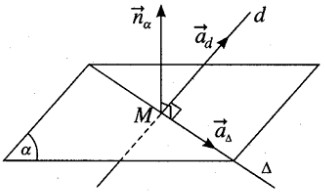
Cho mặt phẳng \((\alpha )\) : 2x + y +z – 1 = 0 và đường thẳng \(d: \frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ - 3}}\)
Gọi M là giao điểm của d và \((\alpha )\) , hãy viết phương trình của đường thẳng Δ đi qua M vuông góc với d và nằm trong \((\alpha )\).
Phương trình tham số của đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = t}\\
{z = - 2 - 3t}
\end{array}} \right.\)
Xét phương trình:
\(2(1 + 2t) + (t) + ( - 2-3t)-1 = 0 \Leftrightarrow 2t-1 = 0 \Leftrightarrow t = \frac{1}{2}\)
Vậy đưởng thẳng d cắt mặt phẳng \((\alpha )\) tại điểm \(M\left( {2;\frac{1}{2}; - \frac{7}{2}} \right)\).
Ta có vecto pháp tuyến của mặt phẳng \((\alpha )\) và vecto chỉ phương của đường thẳng d lần lượt là \(\overrightarrow {{n_\alpha }} = (2;1;1)\) và \(\overrightarrow {{a_d}} = (2;1; - 3)\).
Gọi \(\overrightarrow {{a_{\rm{\Delta }}}} \) là vecto pháp tuyến của Δ, ta có \(\overrightarrow {{a_\Delta }} \bot \overrightarrow {{n_\alpha }} \) và \(\overrightarrow {{a_\Delta }} \bot \overrightarrow {{a_d}} \).
Suy ra \(\overrightarrow {{a_{\rm{\Delta }}}} = \overrightarrow {{n_\alpha }} \wedge \overrightarrow {{n_d}} = ( - 4;8;0)\) hay \(\overrightarrow {{a_{\rm{\Delta }}}} = (1; - 2;0)\)
Vậy phương trình tham số của Δ là \(\left\{ {\begin{array}{*{20}{c}}
{x = 2 + t}\\
{y = \frac{1}{2} - 2t}\\
{z = - \frac{7}{2}}
\end{array}} \right.\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
