Bài tập 11 trang 93 SGK Hình học 12

Bài tập 11 trang 93 SGK Hình học 12

Phương pháp:

• \(\Delta\) vuông góc với mặt phẳng toạ độ (Oxz) nên sẽ nhận VTPT của mặt phẳng (Oxz) làm VTCP. Như vậy ta chỉ cần tìm một điểm thuộc \(\Delta\) thì ta sẽ viết được phương trình.
• Giả sử M và M' và giao điểm của \(\Delta\) với d và d' thì \(\overrightarrow {MM'}\) sẽ cùng phương với VTCP của \(\Delta\).

Lời giải:

Ta có lời giải chi tiết bài 11 như sau:

​​

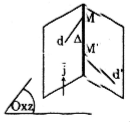
\(\Delta\) vuông góc với mặt phẳng tạo độ (Oxz) nên \(\Delta\) có vecto chỉ phương là \(\vec{j}=(0;1;0)\)

Gọi M(t;-4+t; 3 -t) và M'(1-2t'; -3+t'; 4 - 5t') lần lượt là giao điểm của \(\Delta\) của d và d' (h.34) ta có: \(\overrightarrow{MM'}=k.\vec{j}\)

Suy ra: \(\left\{\begin{matrix} 1-2t'-t=0 \ \ (1)\\ 1+t'-t=k \ \ (2)\\ 1-5t'+t=0 \ \ (3) \end{matrix}\right.\)

Từ (1) và (3) suy ra: \(\left\{\begin{matrix} t=\frac{3}{7}\\ \\ t'=\frac{2}{7} \end{matrix}\right.\)

Thay \(t=\frac{3}{7}\) vào toạ độ M ta được \(M(\frac{3}{7}; -\frac{25}{7};\frac{18}{7})\)

Vậy phương trình tham số của đường thẳng \(\Delta\) là: \(\left\{\begin{matrix} x=\frac{3}{7}\\ \\ y=-\frac{25}{7}+t\\ \\ z=\frac{18}{7} \end{matrix}\right.\)

-- Mod Toán 12