Bài tập 22 trang 90 SGK Hình học 12 NC

Bài tập 22 trang 90 SGK Hình học 12 NC

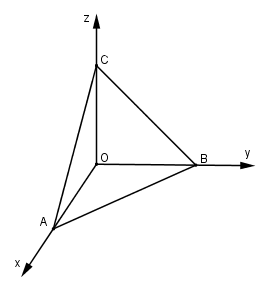
a) Chọn hệ trục tọa độ Oxyz như hình vẽ.

Ta có A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a > 0, b > 0, c > 0) (a > 0, b > 0, c > 0)

Ta có 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB}  = ( - a;b;0);\overrightarrow {AC}  = ( - a;0;c)\\
 \Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = {a^2} > 0
\end{array}\\
{ \Rightarrow cosA = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} > 0}
\end{array}\)

⇒ A là góc nhọn

Tương tự các góc B, C của tam giác ABC cũng nhọn.

b) Mp(ABC) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)

Nên có vecto pháp tuyến \(\vec n = \left( {\frac{1}{a};\frac{1}{b};\frac{1}{c}} \right)\)

Mp(OBC) ≡ Mp(Oyz) có vectơ pháp tuyến \(\vec i = \left( {1;0;0} \right)\)

Gọi α là góc giữa mp(ABC) và mp(OBC) thì:

\({\cos ^2}\alpha  = {\left( {\frac{{\overrightarrow n .\overrightarrow i }}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow i } \right|}}} \right)^2} = \frac{{\frac{1}{{{a^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}\)

Tương tự 

\(\begin{array}{l}
{\cos ^2}\beta  = \frac{{\frac{1}{{{b^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}};\\
{\cos ^2}\gamma  = \frac{{\frac{1}{{{c^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}
\end{array}\)

Vậy \(co{s^2}\alpha  + co{s^2}\beta  + co{s^2}\gamma  = 1\)

-- Mod Toán 12