Bài tập 3.40 trang 130 SBT Hình học 12
Bài tập 3.40 trang 130 SBT Hình học 12
Cho điểm M(2; -1; 1) và đường thẳng \({\rm{\Delta }}:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{2}\)
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng Δ;
b) Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng Δ.
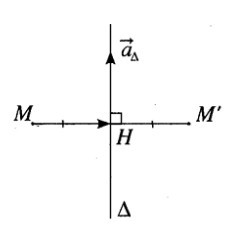
a) Phương trình tham số của \({\rm{\Delta }}:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = - 1 - t}\\
{z = 2t}
\end{array}} \right.\)
Xét điểm \(H(1 + 2t; - 1 - t;2t) \in {\rm{\Delta }}\)
Ta có \(\overrightarrow {MH} = (2t - 1; - t;2t - 1)\)
\(\overrightarrow {{a_{\rm{\Delta }}}} = (2; - 1;2)\)
H là hình chiếu vuông góc của M trên \({\rm{\Delta }} \Leftrightarrow \overrightarrow {MH} .\overrightarrow {{a_{\rm{\Delta }}}} = 0\)
\( \Leftrightarrow 2(2t - 1) + t + 2(2t - 1) = 0 \Leftrightarrow t = \frac{4}{9}\)
Ta suy ra tọa độ điểm \(H\left( {\frac{{17}}{9};\frac{{ - 13}}{9};\frac{8}{9}} \right)\)
b) H là trung điểm của MM’, suy ra xM’ + xM = 2xH
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = \frac{{34}}{9} - 2 = \frac{{16}}{9}\)
Tương tự, ta được \({y_{M'}} = 2{y_H} - {y_M} = \frac{{ - 26}}{9} + 1 = \frac{{ - 17}}{9};\)
\({z_{M'}} = 2{z_H} - {z_M} = \frac{{16}}{9} - 1 = \frac{7}{9}\)
Vậy \(M'\left( {\frac{{16}}{9};\frac{{ - 17}}{9};\frac{7}{9}} \right)\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
